当关键字是有界范围内的整数时，能够规避Ω(lglgn)下界的限制，那么在类似的场景下，我们应弄清楚o(lgn)时间内是否可以完成优先队列的每个操作。在本章中，我们将看到：van Emde Boas树支持优先队列操作及一些其他操作，每个操作最后情况运行时间为O(lglgn)。而这种数据结构限制关键字必须为0~n-1的整数且无重复。

下面以n为元素个数，u为全域大小。

20.1 基本方法

直接寻址

即位图bitmap方法。

insert，delete和member：复杂度O(1)

minimum，maximum，successor和predecessor最坏情况为O(u)

叠加的二叉树结构

位向量的全部元素组成了二叉树的叶子，并且每个内部结点为1当且仅当其子树中任一个叶节点包含1。

 

由于树的高度为lgu，每个操作至多沿树进行一趟向上和一趟向下的过程，因此每个操作的最坏情况运行时间为O(lgn)。

叠加的一棵高度恒定的树

叠加的树度数为u^1/2。每个操作中，最多对两个大小为u^1/2位的簇以及summary数组进行搜索，所以每个操作耗费O(u^1/2)时间。（比二叉树渐进差）

使用度为u^1/2的树是van Emde Boas树的关键思想。

20.2 递归结构

在本节中，我们对位向量上度为u^1/2的叠加树想法进行修改。上一节中，用到了大小为u^1/2的summary数组，数组的每项都指向一个大小为u^1/2的另一个结构。现在使用结构递归，每次递归都已平方根大小缩减全域。（u，u^1/2，u^1/4，u^1/8，...）

通过变量替换法，能够得到递归式

T(n)=2T([u^1/2])+lgn

的解为T(n)=O(lgnlglgn)。考虑一个相似但更简单的递归式：

T(n)=2T(u^1/2)+1

其解为T(n)=O(lglgn)。此递归式将指导数据结构上的查找。我们要设计一个递归的数据结构，该数据结构每层以u^1/2为因子缩减规模。当一个操作遍历这个数据结构时，在递归到下一层次前，其在每一层耗费常数时间。

20.2.1 原型van Emde Boas结构

有些操作达不到O(lglgn)。

MEMBER：O(lglgu)

MINIMUN：O(lgu)

SUCCESSOR：O(lgulglgu)

INSERT：O(lgu)

DELETE：添加一个属性n来记录其拥有的元素个数

20.3 van Emde Boas树及其操作

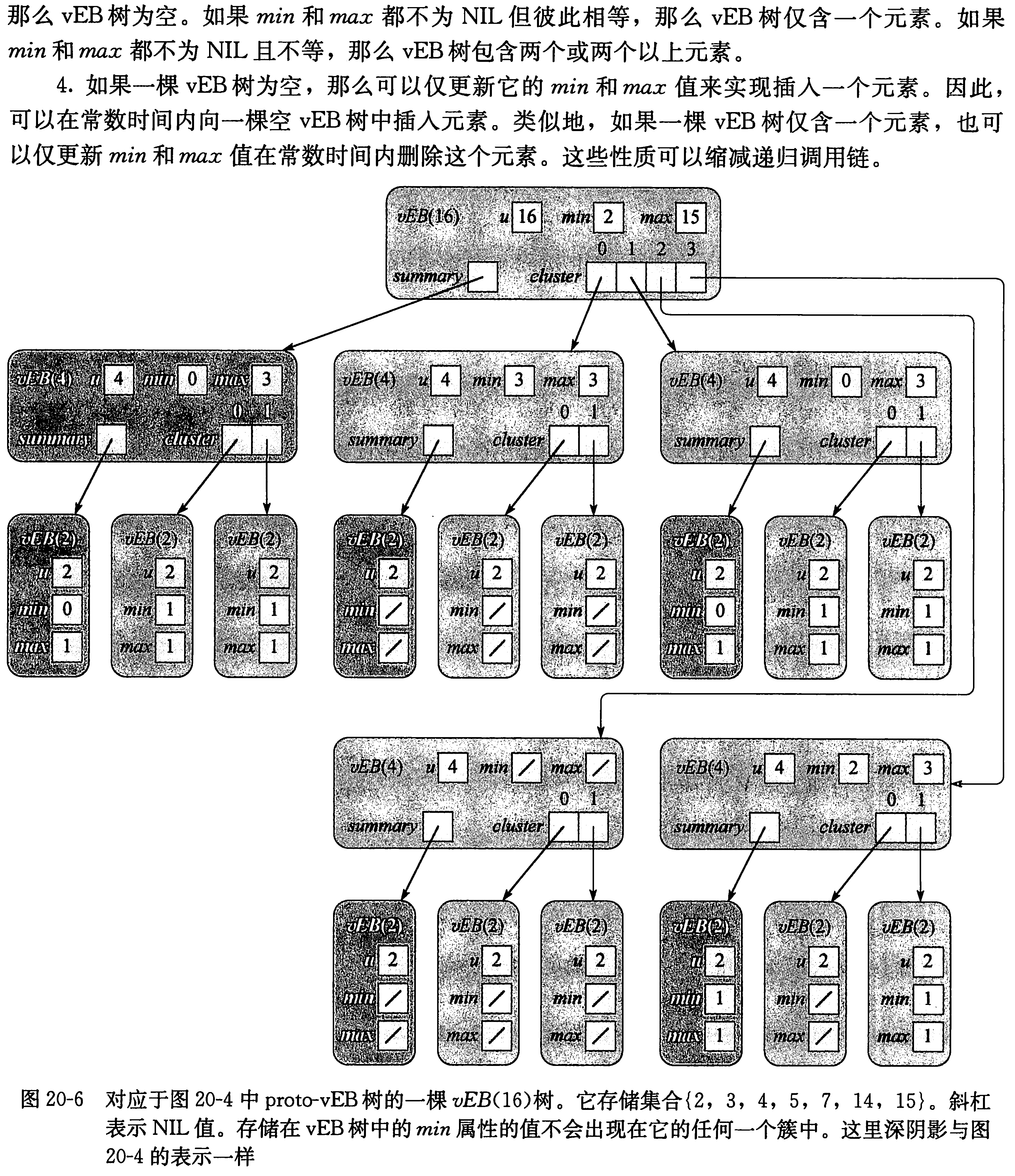
全域限制放宽到2^k，增加两个属性min和max，分别记录vEB树中的最小和最大元素。而且min不出现在在任何cluster中。

得到T(u)=O(lglgn)。

SUCCESSOR：

INSERT：

DELETE：